We study mathematical theories of tensors and hypergraphs, computational algorithms, and their implementation on GPU and FPGA based parallel processors, and applications of tensor computing to machine learning, image analysis, biology, and medicine. We have close collaborations with mathematicians, biologists, and medical doctors.
Click here to see a collection of media reports
Collaborative Research Fund (CRF): Efficient Algorithms and Hardware Accelerators for Tensor Decomposition and Their Applications to Multidimensional Data Analysis.
Project investigators: Hong Yan (EE, CityU), Raymond Chan (Math, CUHK/CityU), Ray Cheung (EE, CityU), Victor Lee (Clinical Oncology, Queen Mary Hospital and HKU Faculty of Medicine), Michael NG (Math, HKBU), Liqun Qi (Applied Math, PolyU)
Click here to see fund information on RGC website (Project C1007-15G).
Click here to see project abstract on RGC website (Project C1007-15G).
 |
Center for Intelligent Multidimensional Data Analysis |
IEEE Award: Professor Hong Yan received the 2016 Norbert Wiener Award from IEEE Systems, Man and Cybernetics Society for contributions to image and biomolecular pattern recognition techniques.
Click here to see the award certificate.
Click here to see CityU news report.
Rising Star: Dr. Chungfeng Cui was recognized as a Rising Star in Computational and Data Sciences in the US in 2019. She was a postdoctoral fellow working in our group and is the first author of the following paper: C. Cui, Q. Li, L. Qi, and H. Yan, "A quadratic penalty method for hypergraph matching," Journal of Global Optimization, 70(1):237-259, 2018.
Click here to visit the Rising Star website.
ACM Competition: Two students Ali Raza Shahid and Frank Xinqi Fan supervised by Professor Hong Yan won the Second Place in Facial Micro-expression Challenge during ACM Multimedia 2021.
Click here to see CIMDA news report.
US NAI Fellowship: Professor Hong Yan has been elected Fellow of the US National Academy of Inventors (NAI).
Click here to see CityU news report.
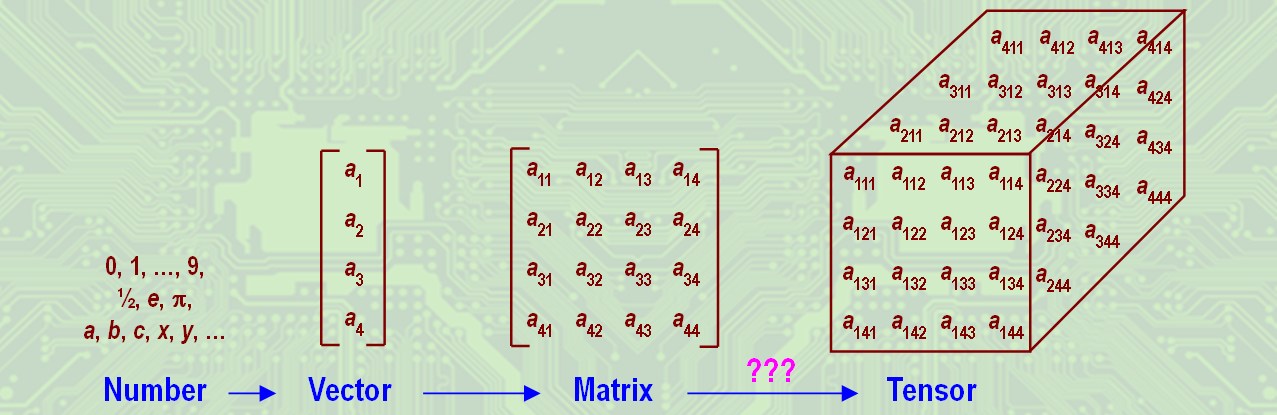
A frequently asked question is why we need tensor models because matrix theories are well developed. Before we answer this question, let us ask you why we need matrices because we can use vectors, and why do we need vectors because we can use numbers directly. We're all back to the stone age of numbers!
If we stack columns of a matrix as a large vector, the 2D intrinsic structure reflected by the matrix may be lost. Just think about a matrix representing the image of a human face. We would not be able to see a meaningful pattern if we convert the matrix to a vector. For the same reason, if we unfold a tensor into a matrix, then the 3D intrinsic structures in the data may be lost. Thus, we need new concepts, mathematical theories, and computer algorithms to analyze higher-order tensors.
Tensor decomposition is a key problem in tensor computing. Methods for matrix decomposition are well understood in numerical analysis, including lower-upper (LU) decomposition, QR decomposition, and singular value decomposition (SVD). Standard software libraries, such as LINPACK and EISPACK, which are now superseded by LAPACK, are available. "Are there analogues to the SVD, LU, QR, and other matrix decompositions for tensors (i.e., higher-order or multiway arrays)?" asked by M. E. Kilmer and C. D. M. Martin in their paper "Decomposing a tensor" (SIAM News, 37(9), 2004).
Extension of matrix theories and computational methods to tensors are not straight forward. For example, for a matrix, a singular vector corresponding to a larger singular value provides a better approximation of the matrix than a singular vector corresponding to a smaller singular value. By setting small singular values to zero, we can obtain an optimal low-rank approximation of the matrix. However, this property is no longer valid for tensors in general.
As pointed out by Kilmer and Martin, "First, there are important theoretical differences between the study of matrices and the study of tensors. Second, efficient algorithms are needed, for computing existing decompositions as well as those yet to be discovered."